Rates Models & Yield

1. The Interest Mechanism

$M token operates within a balanced interest system in the M0 Protocol:

1. Minter Interest Accrual: Minters accrue obligations at the minter rate on their outstanding $M balances.
2. Earner Interest Accrual: Simultaneously, approved earning accounts accrue additional tokens at the earner rate.
3. Rate Synchronization: The EarnerRateModel ensures the earner rate is calibrated so total earnings never exceed total minter obligations (see Rate Model section below for further details).
4. Continuous Mechanism: Both sides update through independent but synchronized continuous indexing systems.

This creates a mathematically balanced system where earner yields are safely constrained by the protocol's income from minters.

$M token implements sophisticated interest rate models that ensure financial soundness while distributing yield between minters, earners, and the protocol.

2. Rate Model Architecture

The protocol uses two primary rate models:

1. MinterRateModel: Determines the interest rate minters pay on borrowed $M token
   • Simple model that reads rates directly from the TTG Registrar
   • Capped at 400% APR (40,000 basis points) for system safety
   • Governance-controlled through the base_minter_rate parameter
2. EarnerRateModel: Calculates the interest rate paid to $M token holders who opt in to earning
   • Uses a mathematical formula that ensures financial soundness
   • Rates are capped at 98% of the calculated safe rate
   • Governed through the max_earner_rate parameter

Minter Rate Calculation

The MinterRateModel has a straightforward implementation:

function rate() external view returns (uint256) {
    return min(TTGRegistrar.get("base_minter_rate"), MAX_MINTER_RATE);
}

• The rate is governance-controlled through the TTG Registrar
• Has a hard cap of 400% APR to prevent system abuse
• Changes to this rate affect all minters uniformly

Earner Rate Calculation

The EarnerRateModel employs a more complex approach to ensure system solvency:

function rate() external view returns (uint256) {
    return min(
        maxRate(),
        getExtraSafeEarnerRate(
            totalActiveOwedM,
            totalEarningSupply,
            minterRate
        )
    );
}

Where:

• getExtraSafeEarnerRate applies the rate multiplier to the safe earner rate
• RATE_MULTIPLIER is 9,800 (98% in basis points)
• ONE is 10,000 (100% in basis points)
• maxRate() returns the governance-set maximum earner rate

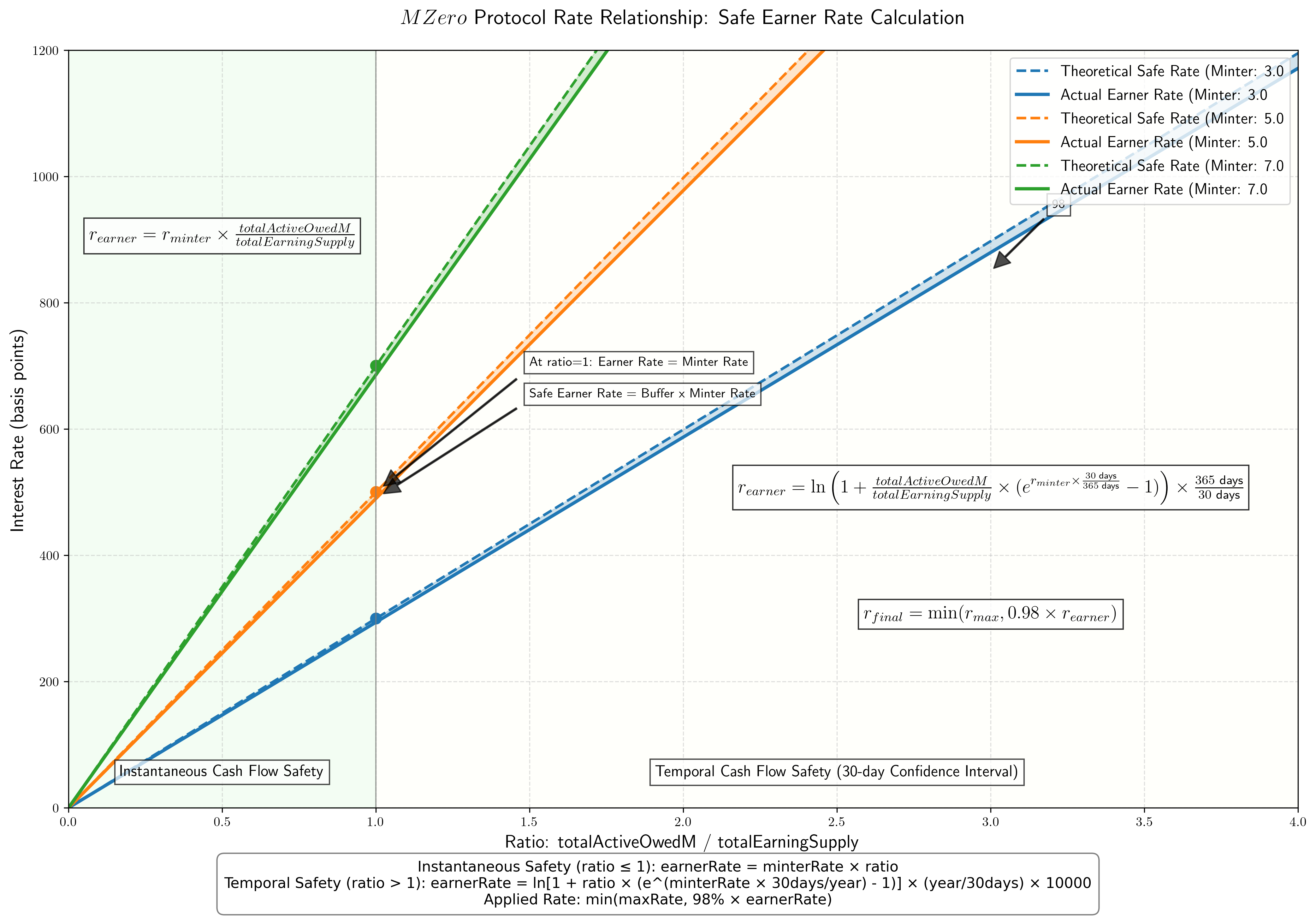
Safe Rate Derivation

The safe earner rate is calculated using two different approaches based on the relationship between total active owed M and total earning supply:

1. When totalActiveOwedM ≤ totalEarningSupply:
   • Uses an instantaneous cashflow approach
   • safeRate = totalActiveOwedM × minterRate / totalEarningSupply
   • Ensures interest paid to earners never exceeds interest collected from minters
2. When totalActiveOwedM > totalEarningSupply:
   • Uses a time-integrated approach over a 30-day confidence interval
   • Accounts for compound interest effects
   • Applies complex mathematical formula to ensure long-term solvency
   • Allows earner rate to temporarily exceed minter rate while maintaining system safety

Extra Safety Factor

The EarnerRateModel applies an additional safety factor to the calculated safe rate:

function getExtraSafeEarnerRate(
    uint240 totalActiveOwedM_,
    uint240 totalEarningSupply_,
    uint32 minterRate_
) public pure returns (uint32) {
    uint256 safeEarnerRate_ = getSafeEarnerRate(totalActiveOwedM_, totalEarningSupply_, minterRate_);
    uint256 extraSafeEarnerRate_ = (safeEarnerRate_ * RATE_MULTIPLIER) / ONE;
 
    return (extraSafeEarnerRate_ > type(uint32).max) ? type(uint32).max : uint32(extraSafeEarnerRate_);
}

This ensures that earners receive 98% of the theoretically safe rate, creating an additional buffer for protocol safety.

Confidence Interval Approach

The EarnerRateModel uses a 30-day confidence interval to determine safe rates:

• Calculates the amount of interest minters will generate over 30 days
• Derives maximum earner rate that ensures total interest paid doesn't exceed this amount
• Accounts for the compounding effects of continuous interest
• Assumes the updateIndex() function will be called at least once every 30 days

Balance Between Minters and Earners

The system maintains a mathematical relationship between interest flows:

totalInterestFromMinters = totalActiveOwedM × (e^(minterRate×Δt) - 1)
totalInterestToEarners = totalEarningSupply × (e^(earnerRate×Δt) - 1)

The rate models ensure: totalInterestToEarners ≤ 98% of totalInterestFromMinters

Edge Cases Handling

The EarnerRateModel handles several edge cases with special logic:

• When totalActiveOwedM = 0 or minterRate = 0: The earner rate is set to 0
• When totalEarningSupply = 0: The earner rate is set to the maximum possible value (type(uint32).max)
• When calculations might overflow: The implementation includes safeguards against numerical issues

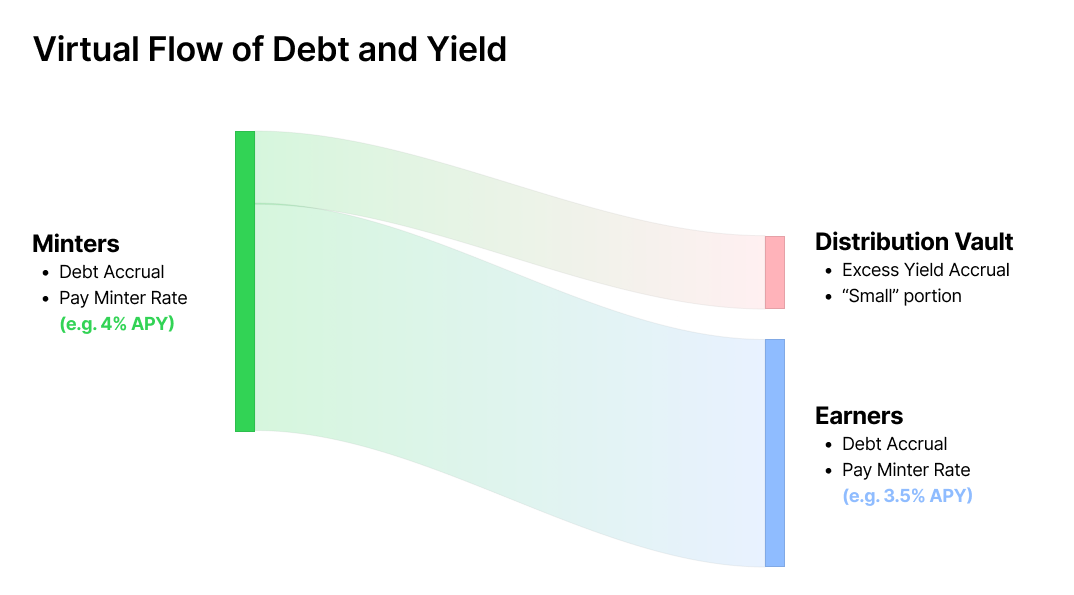
Yield Distribution

The system distributes yield in the following manner:

1. Minters pay interest based on their outstanding debt at the minter rate
2. Earners receive up to 98% of the available interest (subject to constraints)
3. Excess yield (at least 2% plus any additional buffer) goes to the TTG Vault
4. The TTG Vault funds protocol operations and can distribute to governance token holders

Rate Update Mechanism

Interest rates don't change automatically when governance parameters are updated:

1. Rate changes in the TTG Registrar take effect only when updateIndex() is called
2. Both $M token and MinterGateway must update their respective indices
3. Updates occur automatically during key operations such as minting, burning, and transfers
4. Rate models recalculate rates during each update based on current system state

Mathematical Precision

The implementation includes several technical considerations:

• Rates are stored in basis points (1/100 of a percent) for precision
• Calculations use fixed-point math with 12 decimal places (1e12 scaling)
• Exponential calculations use Padé approximants for gas-efficient computation
• Conservative rounding strategies favor protocol safety

Visuals